Linear vs Logistic
선형과 비선형, 그리고 로지스틱
이번 포스팅에서는 선형 회귀와 로지스틱 회귀에 대해 설명드리고자 합니다. 제가 처음 머신러닝을 공부할 때, 다소 헷갈렸던 개념입니다. 우선 먼저 집고 넘어갈 부분은 다음과 같습니다.
- 우리가 자주 접하는 Logistic regression model은 비선형(Non-linear)이다.
- 우리가 자주 접하는 Linear regression model은 선형(linear)이다.
- 딥러닝 모델들은 비선형(Non-linear)이다.
위의 1~3의 정의는 그냥 받아들인다는 생각으로 여러번 읽어보겠습니다.
선형? 회귀? 선형 결합? 모르는 단어들이 많죠. 한번 하나하나 짚어보겠습니다.
-
- 회귀란?
- 데이터 패턴을 파악해서, 그 패턴을 표현해 줄 수 있는 함수를 구해보려 하는 것.
- 회귀란?
-
- 선형 회귀(Linear Regression) 분석이란?
- 관찰된 데이터를 바탕으로 함수를 구한다. 그 함수를 이용해서 관찰되지 않은 데이터의 값들을 예측하는 것
- 선형 회귀(Linear Regression) 분석이란?
-
- 회귀 계수란?
- 회귀 분석을 하기 위해 구한 함수가 y=ax1 + bx2라고 가정하자. 여기서 회귀 계수는 a,b이다.
- 회귀 계수란?
-
- 선형 회귀 모델이란?
- 회귀 계수를 선형적으로 결합할 수 있는 모델
- 선형 회귀 모델이란?
-
- 선형적으로 결합?
- Linear Combination이라고 부르며, 벡터들을 스칼라 곱셈, 벡터와의 덧셈 등을 조합하여 새로운 백터를 얻는 연산
(스칼라는 쉽게 생각해서 숫자라 생각하면 됩니다)
위의 y=ax1 + bx2로 예를 들면, a와 b계수는 x1과 x2와 곱해져서 y를 얻는 연산을 하였습니다.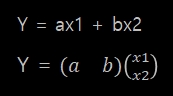
- 선형적으로 결합?
자 그럼, 단어의 정의들에 대해서 설명은 마쳤으니 각 모델의 특징을 살펴보겠습니다.
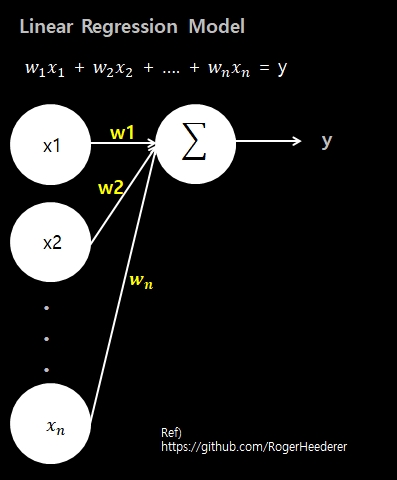
- 선형 회귀 모델은 최적의 w와 b를 찾기 위해 비용함수 MSE를 활용하여 경사하강법을 수행합니다.
- 회귀 계수가 선형결합인 함수의 MSE를 계산해보면 볼록한(convex) 모양이기 때문에 경사하강법으로 최소 지점을 찾을 수 있습니다.
- 선형 회귀의 결과값은 수치값으로 나오기 때문에, 참 또는 거짓을 분류하는 이진분류 문제에 적합하지 않습니다.
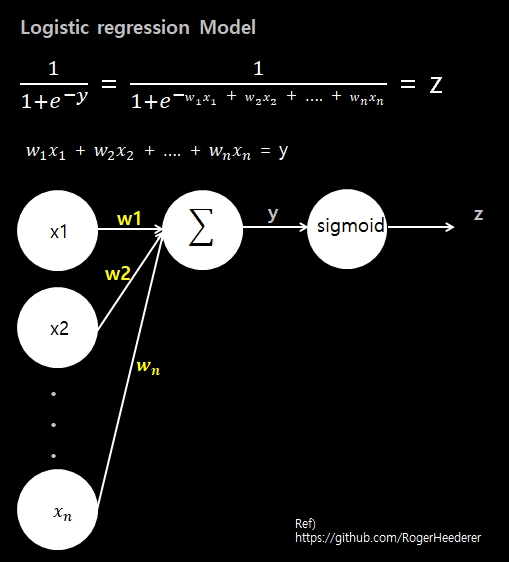
- 로지스틱 회귀 모델은 선형 회귀에서 나온 결과값(수치)을 받아서, 특정 레이블(참, 거짓)로 분류하는 모델입니다.
- 로지스틱 회귀 모델은 최적의 w와 b를 찾기 위해 비용함수 크로스 엔터로피를 활용하여 경사하강법을 수행합니다.
- 이 모델의 회귀 계수는 위의 사진처럼 선형 결합이 안됩니다. 위의 예제처럼 벡터로 표현할 수 없죠. 회귀 계수가 비선형결합 형태인 함수의 MSE를 계산해보면 볼록한 모양이 나오지 않고, 구불구불한 굴곡이 있는 모양이 나오기 때문에, MSE를 활용한 경사하강법으로는 최소 지점을 찾을 수 없습니다. 즉 로컬 미니멈 문제를 가지고 있기 때문에 MSE는 로지스틱 회귀에 적합한 비용함수가 아닙니다.