Long Tail Problem

Long Tail Problem

이번 포스팅에서는 머신 러닝 분야에서 언급되는 Long Tail Problem 대해 알아보고자 합니다. 이미지 처리 분야, 자연어 처리 분야에서 다루는 트레이닝 데이터 셋과 관련하여 나오는 용어입니다.

우선, Long Tail이라는 단어는 2004년에 경제 도메인에서 유래한 단어입니다. 혹시 파레토 법칙은 들어보셨나요? 상위 20% 고객이 매출의 80%를 창출한다. 뭐 이런 의미입니다.

Long Tail 법칙은 파레토 법칙과는 반대로, 80%의 사소한 다수가 20%의 핵심 소수보다 뛰어난 가치를 창출한다는 이론입니다. 역 파레토 법칙이라고도 부르는데요, 아래 그림을 한번 보시죠.

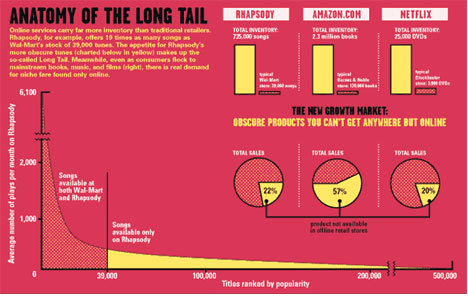
Head 파트에 위치한 소수의 제품들이 많이 팔리고, 그 이외의 다수의 제품들의 판매량이 떨어지면서 긴 꼬리처럼 낮고 길게 늘어져 있습니다. 얼핏 보면 20%의 Head 파트의 소수 제품들의 판매량이 많은 것처럼 보이지만,실제로는 꼬리에 위치한 80% 다수의 제품 판매량이 머리에 위치한 소수 제품 판매량을 뛰어 넘습니다.

원론적인 이론 설명에 대해서는 여기까지 하고, CS 도메인에서 이어 설명하겠습니다.

사실 이 Long Tail Problem이 NLP 분야에서 어떤 개념으로 활용되는지에 대해 찾기가 힘들었습니다. 그러다가 우연찮게, Vision 분야와 관련된 논문에서 위 개념을 파악할 수 있었습니다.

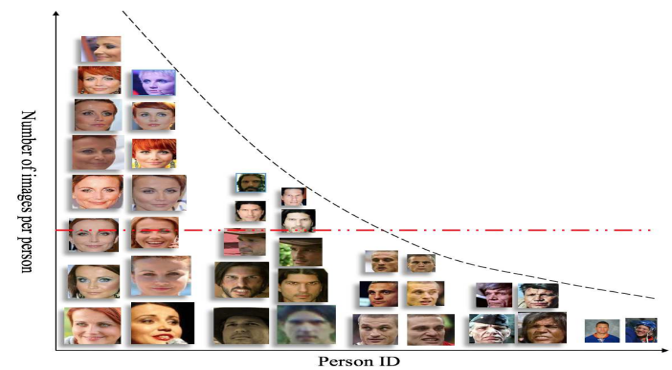
“Range Loss for Deep Face Recognition with Long-Tailed Training Data” ICCV 2017.

아래 사진은 MS-Celeb-1M 데이터 셋에 들어 있는 사진 일부들을 분포화 시켜놓은 그래프입니다. 가로축은 각각의 인물들을 나타내며, 세로축은 각 인물들에 대한 사진의 갯수를 나타냅니다. 위 사진에 등장하는 인물의 숫자는 총 10명입니다. 그런데 각 인물을 나타내는 사진의 개수가 차이가 납니다. 첫번째 등장하는 여자 인물 사진은 8개. 마지막 남자의 사진은 1개입니다.

즉, Head에 위치한 데이터들은 샘플이 많고, Tail에 위치한 데이터들의 샘플은 적습니다. 이처럼 머신러닝 분야에서는, Head data samples과 Tail data samples이 불균형하게 분포되어 발생되는 문제를 ‘Long Tail Problem’이라 부릅니다.

그럼 어떤 문제가 발생하는냐?? 이에 대한 설명은 NLP 도메인의 예시로 설명하겠습니다.

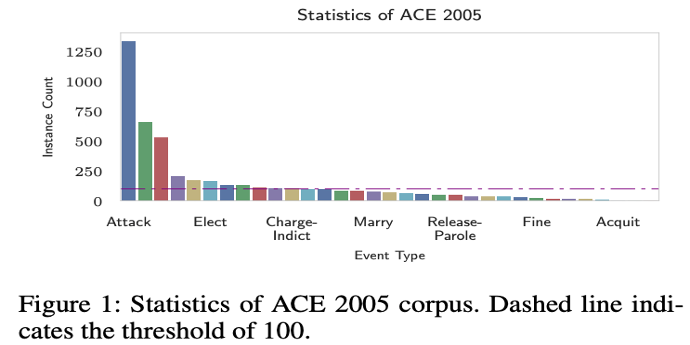
“Event Detection via Gated Multilingual Attention Mechanism” AAA 2018.

이 그림은 위 논문의 실험에 활용하고 있는 ACE2005 데이터 셋의 evnet type 분포 현황입니다. ‘Attack’ 이라는 이벤트 타입을 보면, 압도적으로 많이 등장하는 것을 보실 수 있습니다. Attack, Elect 등 굉장히 자주 등장하는 몇몇 타입들을 제외하고서는 나머지 비핵심 이벤트 타입들은 꼬리처럼 길게 늘어져서 전체 분포의 70% 이상을 차지하고 있는 모습을 확인 할 수 있습니다.

이처럼 불균형한 분포를 가진 데이터에 트레이닝 된 모델이 테스트 시에, 메인 클래스(샘풀이 많은 클래스)overfitting되는 경향이 있습니다. 그리고 비주류 클래스(샘플이 적은 클래스)의 sample data들은 클래스 내부에서 큰 분산, 퍼짐을 보이는 경향이 있습니다. 이런 문제들 때문에 Event Detection 분야에서 Event Triggers를 찾는 성능이 저하되며, 자연스레 이런 결과는 최종 모델의 Performance에 악영향을 주게 됩니다.

그럼 샘플이 적은 꼬리들은 잘라버리면 안되나? 대세에 별 영향력도 없을 것 같은데? 라는 생각을 하실 수도 있습니다. 하지만 앞서 설명한 경제분야의 Long tail 법칙에서 사소한 80%가 큰 영향력을 보여줄 수 있다고 한 것처럼, 위 논문에서는 길게 늘어진 꼬리 데이터들을 적절하게 가다듬는다면, 훈련 모델 성능 향상에 크게 기여할 수 있다고 설명합니다.

p.s) 참고로, 앞선 포스팅에서 설명한 Bootstrap 기법으로 훈련 데이터를 확장하는 방법이 Long Tail Problem을 경감시키는데에 유효한 솔루션으로 보는 관점이 있었습니다. ((Ferguson et al., 2018; Zhang et al., 2019; Cao et al.,2019) 하지만 이 방법은 비슷한 동질성을 가진 샘플들만 생성(Homogeneity)하여, 이게 곧 균등하지 못한 샘플 데이터 분포(Unevenly distributed)를 야기한다고 지적합니다. resampling 하는 타겟 데이터 셋 자체가 편향적이기 때문에(내부적으로 기 형성된 데이터 편향이 존재),bootstrapping 방법론은 Long tail problem을 경감시키기 어렵다고 판단합니다.