Empirical Demonstration of Learning Process
학습 과정의 실제 모습
이번 포스팅에서는 기계가 학습하는 과정을 실증적인 데이터를 통해 표현하여 설명드리고자 합니다.
앞선 포스팅에서 설명한 머신러닝을 읽어보셨나요? 기계가 학습을 통해 판단력, 추론을 가지게 된다고 하였습니다. 그럼 어떻게 학습을 하는 걸까요?? 알고리즘과 데이터를 통해서 패턴을 찾아 학습한다고 하는데, 되게 추상적으로 느껴지실 겁니다. 저 또한 머신러닝 학습 초반에 머리 속에서 구름이 둥둥 떠다니는 느낌을 많이 받았거든요.
‘그래 뭐 스스로 기계가 학습한다는 사실은 알겠는데 그 과정이 눈으로 보여야 말이지… 결과는 딱 나오니 학습을 안한다고 생각할 수는 없는데… 어떻게 내부적으로 학습되고 있는거야?’
자, 이제 머리 속에 떠 다니는 구름을 치워봅시다.
해당 그림과 예시 설명은 봉수골 개발자 이선비(Youtube)님의 자료를 가져왔습니다.
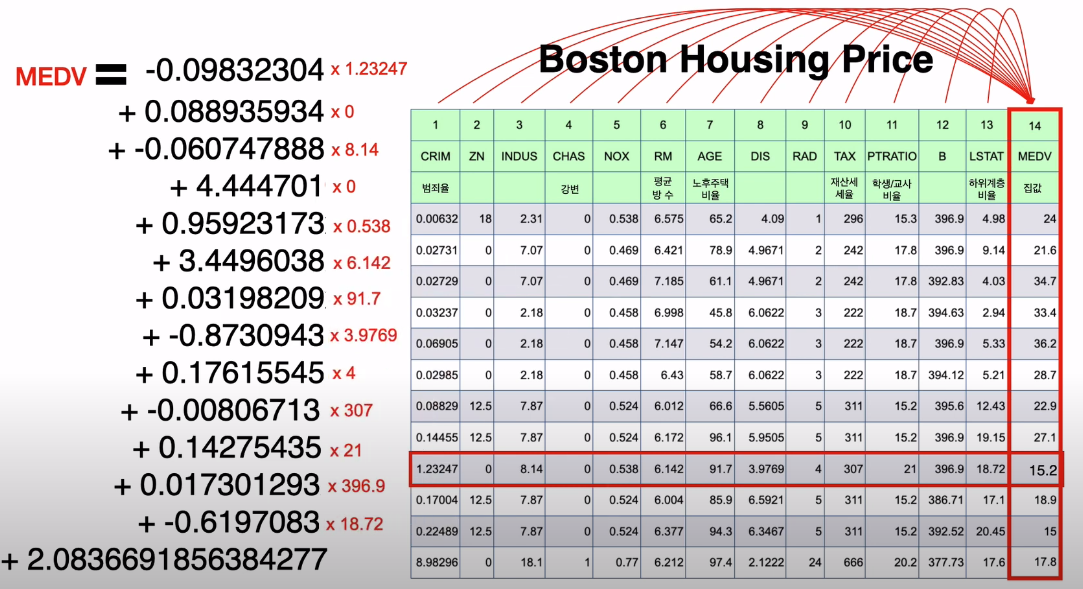
위 그림은 보스턴 집 값에 대한 데이터들을 나열한 표입니다. 12개의 rows는 각각의 집들을 의미하며, 14개의 Columns은 해당 집들의 특성을 의미합니다. 빨간색 네모 박스를 한번 같이 보시죠. CRIM, ZN, … LSTAT. 1~13번까지의 컬럼 요소들이 제일 마지막 14번 MEDV 집값에 영향을 끼치는 구조입니다. 범죄율이 1.23247이고 강변 근처가 아니며(CHAS=0) 평균 방의 갯수는 6.142개이며 등등을 다 고려했을 때 집값이 15.2로 나타나는 것을 확인할 수 있습니다.
즉, MEDV = w1 X CRIM + w2 X ZN + ……. + w13 X LSTAT + bias 로 표현할 수 있습니다. 13개의 독립변수들이 영향을 끼쳐 만들어 낸 1개의 종속변수 MEDV(집값) 입니다.
여기서 기계가 학습하는 것은 바로 w1,w2……w13와 bias. 14개의 값들을 지속적으로 변화시키면서 가장 적합한 값을 찾아내는 것입니다.
1번 집, 2번 집, 3번 집 등을 쭉 계산하여 집값을 예측하고, 예측 집값이 실제 집값과의 차이가 가장 적어지도록 하는 과정.
즉, 최적의 w1 ~ w13, bias 값을 찾아내는 것. 이것이 기계가 학습하는 과정이라고 볼 수 있습니다. 위 사진에서 12개의 집이 있습니다.
- 첫 번째 집이 가진 독립변수들 x1~x13과 종속변수 y의 관계를 학습합니다.
w1 X 0.00632 + w2 X 18 + … w13 X 4.98 = 24
두 번째 집이 가진 독립변수들 x1~x13과 종속변수 y의 관계를 학습합니다.
w1 X 0.02731 + w2 X 0 + … w13 X 9.14 = 21.6
.
.
.
아홉 번째 집이 가진 독립변수들 x1~x13과 종속변수 y의 관계를 학습합니다.
w1 X 1.23247 + w2 X 0 + … w13 X 18.72 = 15.2
.
.
열세 번째 집이 가진 독립변수들 x1~x13과 종속변수 y의 관계를 학습합니다.
w1 X 8.98296 + w2 X 0 + … w13 X 17.6 = 17.8
결국, 기계는 첫 번째부터 열세 번째 집까지의 독립변수들과 종속변수의 계산 과정들을 학습을 한 후, 13개 개별 집값을 평균적으로 가장 잘 예측해줄 수 있는 w1~w13과 bias 값을 찾게 됩니다.
최종적으로 기계가 정한 값들은 사진에 나와있는 -0.09, 0.08, -0.06 …. -0.6이 되고, bias는 2.08이 됩니다. 위 값을 대입해서 아홉 번째의 집값을 구해보면 19.13이 나옵니다.
말로 풀어보자면, 범죄율이 1.23247이고, 강변에 있지 않으며, 평균 방수가 6.142개이고 …. 하위계층비율이 18.72인 실제 집 값은 15.2이다. 반면 기계는 위 조건의 집의 가격을 19.13이라고 더 높게 예측했다. 이런 의미입니다.
자 그럼, 기계가 최종적으로 정한 이 최적의 w,b 값을 어떻게 찾아나가는지 설명드리겠습니다.
해당 그림과 예시 설명은 봉수골 개발자 이선비(Youtube)님의 자료를 가져왔습니다.
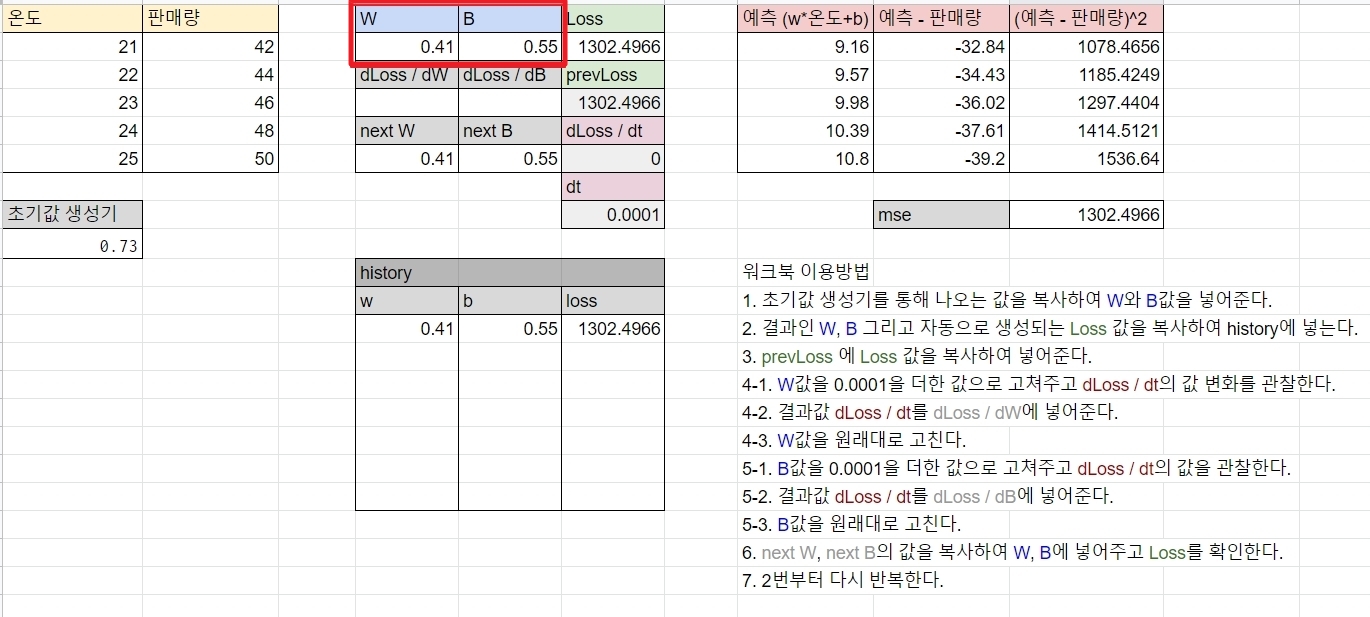
해당 엑셀 파일에는 기계가 실제로 w와 b를 학습하여 수정해나가는 로직이 담겨 있습니다. 그 과정을 차례로 보여드리며, 어떻게 기계가 w와 b를 변경해가며 최종 값으로 정하는지를 설명하겠습니다.
w와 b 값이 0.41, 0.55로 초기 설정되어 있습니다. w,b를 initialize(초기값 설정)하는 방법론은 몇 가지가 있으며, 이 포스팅에서는 해당 방법론은 생략하겠습니다.
초기에 정해진 w와 b값을 통해 계산을 해보았습니다. 첫 loss 값이 1032.49가 나왔습니다. 풀어서 설명해보겠습니다.
- 온도(21) X 0.41 + 0.55 = 9.16(예측판매량)
- 9.16 - 42(실제판매량) = -32.84
- mse(-32.84) = 1078.4656 = loss값
즉 예측 판매량과 실제 판매량의 차이를 mse 취한 값이 loss가 됩니다.
그럼 이 loss값을 더욱 줄이기 위해서는 w와 b값을 다시 정해야 합니다. 즉 더 나은 loss를 위해서 w와 b를 미분하는 수학 공식을 통해, 더 적합한 w와 b를 구해냅니다. dt(미분값) 0.0001만큼 w,b 값을 키워보겠습니다.
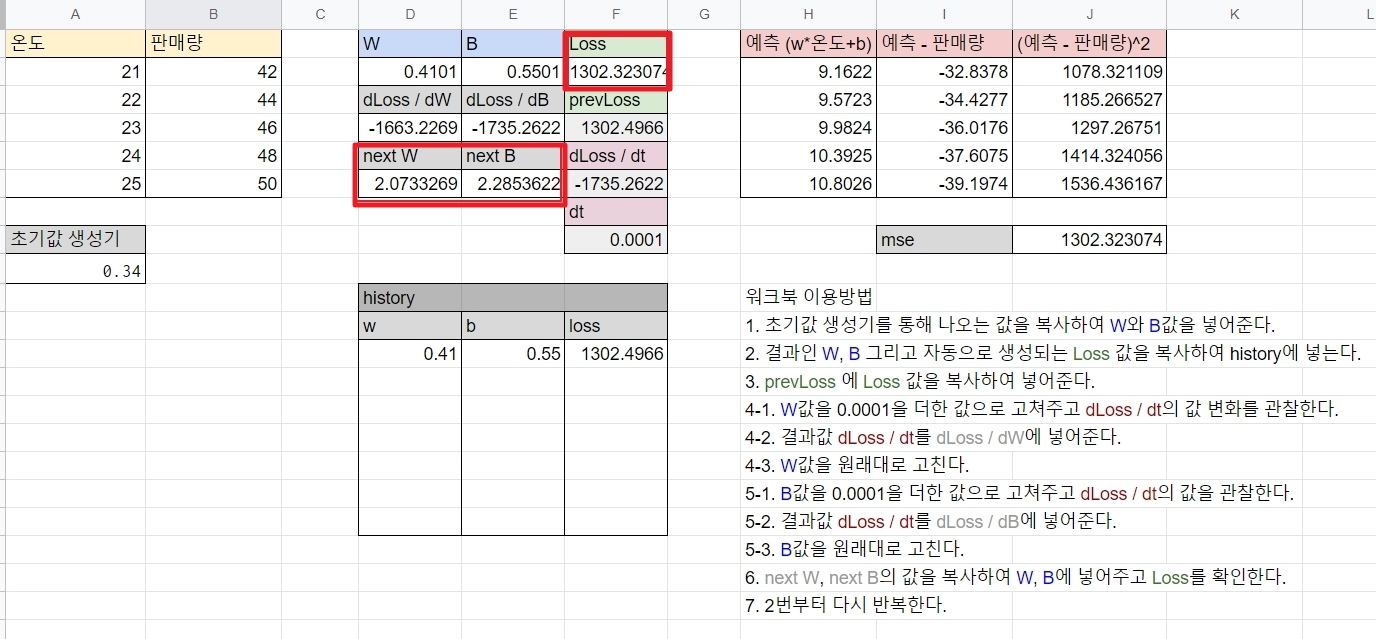
그랬더니, next W, next B 값이 새로 나왔습니다. 이 값을 현재 w,b 값으로 대체하여 넣어보겠습니다.
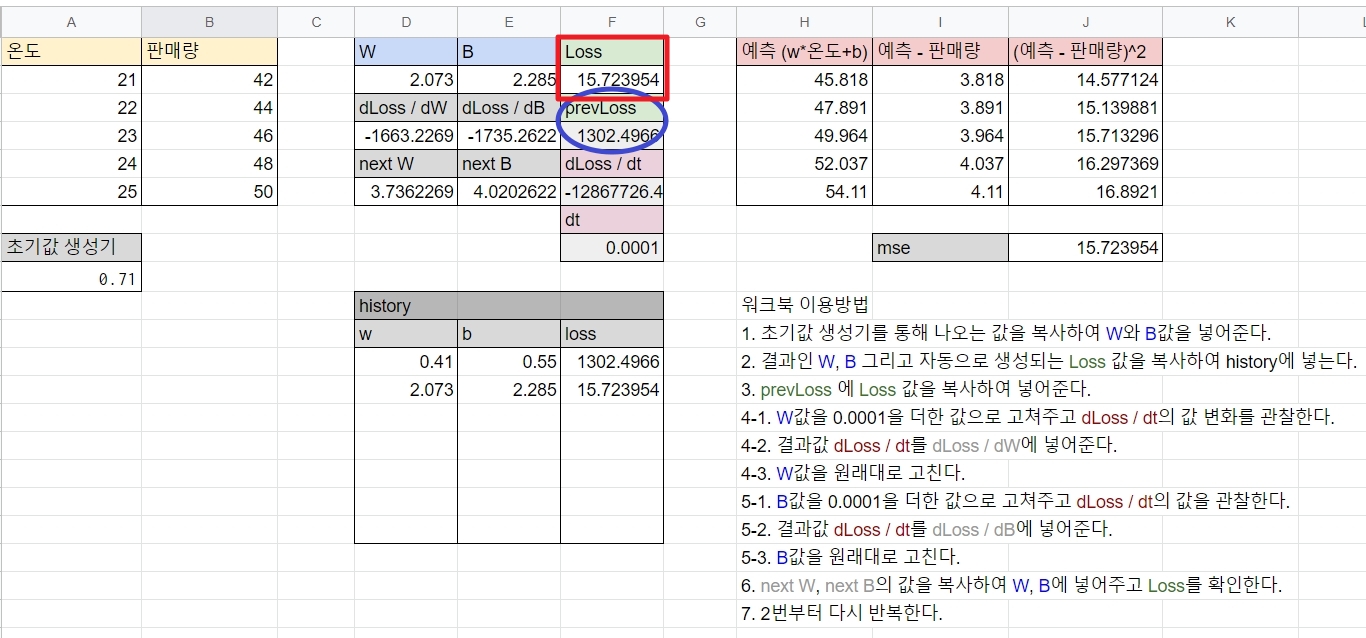
15.72라는 새로운 loss 값을 확인할 수 있습니다. 앞선 1302.49 loss 값보다 현저히 줄은 것을 확인할 수 있습니다.
즉 위의 w와 b값을 늘리거나 줄이는 과정(+0.0001 or -0.0001)을 반복해가며 w와 b의 변화를 살피고, 그에 따라 정해지는 loss 값이 감소하는지 증가하는지의 추이를 함께 살펴보면 됩니다. 감소하고 있다면 학습이 올바르게 되고 있는 것이고, 증가하고 있다면 학습이 문제가 있다는 뜻이 되겠죠.
앞서 설명한 일련의 과정들이 기계가 학습하는 흐름입니다. w,b값을 초기화하고, loss 값을 계산하여 다음 w와 b값을 선정하기 위해 미분을 하며, 그에 따라 나온 새로운 w,b값을 재배정하여 다시 loss 값을 계산하고…
이런 반복되는 알고리즘들은 Tensorflow 프레임워크에 구현되어 있습니다.
저희는 이미 잘 구현된 알고리즘들을 잘 가져다 쓰기만 하면 되지만, 그 전에 이런 원리들을 안다면, 찝찝한 마음 없이 가벼운 마음으로 잘 가져다 쓸 수 있겠죠? 어떤 식으로 기계가 학습하는지 알고 있으니 결과 값에 신뢰감이 들테니까요!!