Knowledge Distillation

지식 증류

이번 포스팅에서는 머신 러닝 분야에서 활용되는 Knowledge Distillation에 대해 알아보고자 합니다. 이 용어는 처음 Distilling the Knowledge in a Neural Network 논문에서 등장했는데요, 지식을 증류한다? 무슨 의미인지 살펴보겠습니다.

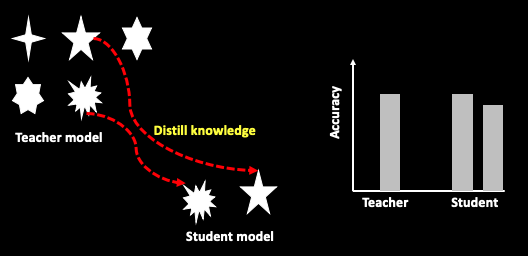
Distillation(증류)는 불순물이 섞여 있는 혼합물에서 원하는 특정 성분을 분리시키는 방법을 뜻합니다. 본 논문에서 말하는 Knowledge Distillation의 개념은 “이미 잘 학습된 Teacher network의 Knowledge(parameters)에서, 필요하지 않은 Knowledge는 제외하고, 성능 향상에 도움이 되는 Knowledge만을 추출(증류)해내어 상대적으로 작은 Student model 학습에 활용하는 것“을 뜻합니다.

즉 선생 모델의 파라미터 개수 > 학생 모델의 파라미터 개수. 즉 모델의 복잡도나 크기는 선생이 더 크지만, 어떤 테스크를 수행함에 있어서 두 모델의 성능 차이는 없도록 하는 것이 Knowledge Distillation의 목적입니다.

좀 더 와닿는 설명을 위해, 예를 들어보겠습니다. 수학을 배운 선생님과 학생이 있습니다. 선생님은 수학을 전공하여 초등학교 기초 수학 과정부터 대학 고급 수학 과정까지 다 배웠습니다. 반면 학생은 초등학교 기초 수학 과정까지만 완벽히 배웠다고 가정하겠습니다. 그리고 선생과 학생에게 시험 문제를 풀라고 제안합니다. 이 시험 문제의 구성은 초등학교 수준의 기초 연산 내용만을 담고 있습니다. 덧셈 3문제. 뺄셈 3문제. 곱셈.3문제 나눗셈 3문제. 이렇게 총 12문제로 구성되어 있습니다. 이 시험의 결과는 선생과 학생 모두 100점을 받았습니다. 시험 문제의 범위가 덧셈 ~ 나눗셈까지였기 때문에, 학생 수준에서도 충분히 풀 수 있었습니다. 반면 선생 입장에서는 자신이 알고 있는 고급 수학 지식들을 전부 활용하지 못하였죠.

위 예시를 모델로 나타내어 보면 아래와 같습니다.
Teacher(Plus, Minus, Multi, Div, Tan, Sin, Cos,……, Vector)
–> Output : Score 100
(Plus 25, Minus 25, Multi 25, Div 25)

Student(Plus, Minus, Multi, Div)
–> Output : Score 100
(Plus 25, Minus 25, Multi 25, Div 25)

선생 모델은 덧셈,뺄셈과 같은 기초적인 Parameter(Knowledge)에서부터 탄젠트, 코사인, 벡터 등의 심화된 Parameter까지 가지고 있습니다. 반면 학생 모델은 덧셈, 뺄셈, 곱셈, 나눗셈까지만 Paramter를 가지고 있습니다. 위 시험 문제를 풀기 위해서는 Student Model도 충분합니다. 즉 작고 덜 복잡한 모델로도 큰 모델만큼의 성능을 얻을 수 있다면, 더 효율적인 방법이 됩니다. 이렇게 Knowledge Distillation은 작은 네트워크로도 큰 네트워크와 비슷한 성능을 낼 수 있도록, 학습 과정에서 큰 네트워크의 지식을 작은 네트워크에 전달하여 적절한 성능을 이끌어 내겠다는 목적을 가지고 있습니다. 그럼 이 지식을 추출하여 전달하는 과정은 어떻게 진행될까요? 이 포스팅에서는 개념적으로만 설명드리고, 자세한 수식은 앞서 언급한 논문을 참조하시면 됩니다.

우선, 선생 모델의 Output(출력물)을 살펴봅니다. 선생 모델은 많은 Knowledge(Parameters)를 가지고 있는데, 실제로 출력물을 보니 ‘Plus, Minus, Multi, Div 파라미터만 있으면 되겠구나..’, 테스크에 맞는 관련 Knowledge(Parameters)만 가져와서 더 가볍고 작은 네트워크를 구성하여 학생 모델을 만든다고 생각하시면 됩니다.

즉, 선생 모델의 출력값을 학생 모델이 모방을 하며, 어떤 Knowledge가 적절한지 판단하여 추출하는 일련의 과정이 Knowledge distillation 방법론입니다.